Quickly and Accurately Determine Your “Circulating Load Ratio”

The typical closed ball milling circuit is shown in Figure 1. The circulating load ratio is known to be an extremely important design/operating parameter, as shown in Figure 2.

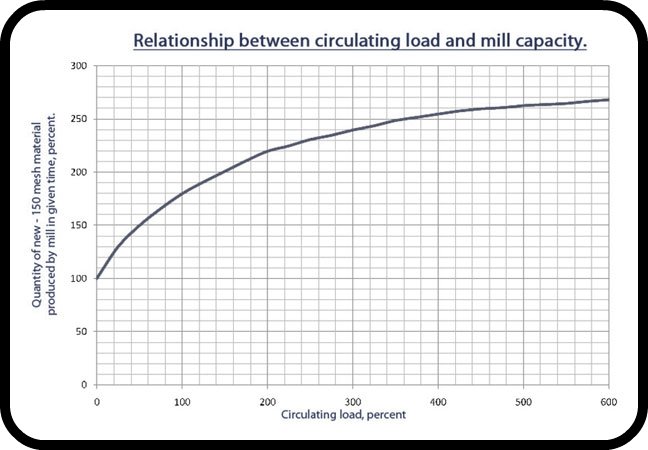
What is the circulating load ratio in your ball milling circuit? There is a rapid and easy way to calculate it from any set of circuit size distribution data for the standard circuit arrangement shown in Figure 1, as follows.

Let’s first clearly define “circulating load ratio” as the ratio of the amount of solids going through the ball mill divided by the amount of solids going through the circuit. As it turns out, a valid “mass-balance” formula can be derived from the following two questions:

Then the circulating load ratio is equal to ‘A’ divided by ‘B’, the number of passes through the mill needed to generate the total amount of new circuit product.

Example:

A ball mill circuit product (cyclone overflow) contains 80% passing 75 um (200 mesh). The circuit feed (from the previous stage of size reduction) contains 20% passing 75 um. Therefore, the circuit is producing 60% (percentage points) of new minus 75 um material (i.e. ‘A’, above, equals 60).

At the same time it was determined that the ball mill feed (cyclone underflow) contains 25% passing 75 um, and the mill discharge contains 45% passing 75 um. Therefore, during each pass through the mill 20% (percentage points) of new minus 75 um material is generated (‘B’, above, equals 20). The circulating load ratio is then 60 divided by 20, thus equal to 3.0, or 300%.

Try this out with any good set of data from the standard circuit arrangement shown above. It works with any screen size you choose to do the calculations. What is sometimes regarded as a perplexing question is readily answered from a set of size distribution data, both quickly and accurately.